Площа бічної поверхні прямої призми обчислюється за формулою
(де Р-периметр основи, h-висота, Sб - площа бічної поверхні, Sосн - площа основи)
Площа поверхні призми обчислюється за формулою
Площа основи прямої призми дорівнює 9 см2, а площа бічної поверхні - 12см2. Знайдіть площу повної поверхні призми.
Установіть відповідність між призмою (1-4) і площею її бічної поверхні (А-Д)
Пряма трикутна призма, основою якої є прямокутний трикутник із катетами 3 см і 4 см, а висота дорівнює 10 см
Пряма призма, основою якої є чотирикутник зі сторонами 6 см, 7 см, 8 см, 9 см, а бічне ребро дорівнює 5 см.
Правильна трикутна призма, діагональ бічної грані якої дорівнює 10 см, а радіус кола, описаного навколо основи, - 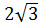 см.
см.
Правильна чотирикутна призма, діагональ якої дорівнює 9 см, а діагональ основи - 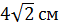
150 см2
112 см2
120 см2
132 см2
144 см2
В основі прямої призми лежить прямокутник зі стороною 6 см і діагоналлю 10 см. Бічне ребро призми дорівнює 20 см. Знайдіть площу повної поверні призми.
(У відповіді записати тільки число)
В основі прямої призми лежить прямокутний трикутник із катетами 6 см і 8 см. Знайдіть площу бічної поверхні призми, якщо її бічне ребро дорівнює 8 см.
(У відповіді записати тільки число)
За якою теоремою можна знайти невідому сторону трикутника, у якому задано дві сторони і кут між ними?
За якою теоремою можна знайти невідому сторону трикутника, у якому задано одну сторону і кути, один з яких лежить проти відомої сторони, а інший – проти невідомої?
Використовуючі теорему косинусів або теорему синусів знайдіть невідомий елемент трикутника і встановіть відповідність.
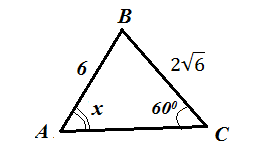
Використовуючі теорему косинусів або теорему синусів знайдіть невідомий елемент трикутника і встановіть відповідність.
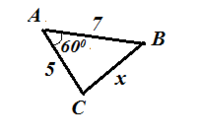
Обчисліть радіус кола, описаного навколо трикутника, якщо один із його кутів дорівнює 60°, а протилежна йому сторона — 60 см.
У трикутнику проти більшої сторони лежить...
Користуючись теоремою косинусів для трикутника АВС, виберіть правильне твердження.
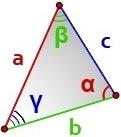
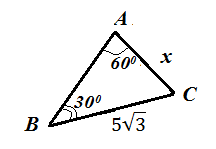 Використовуючи теорему косинусів або теорему синусів знайдіть невідомий елемент
Використовуючи теорему косинусів або теорему синусів знайдіть невідомий елемент
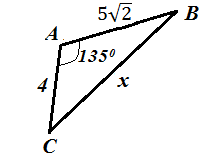 Використовуючи теорему косинусів або теорему синусів знайдіть х2
Використовуючи теорему косинусів або теорему синусів знайдіть х2
Комментариев нет:
Отправить комментарий